Fully coherent search on glitching data using MCMC

This example applies the basic fully coherent search using MCMC, to the glitching signal data set created in make fake data. The aim here is to illustrate the effect such a signal can have on a fully-coherent search. The complete script for this example canbe found here.

After importing pyfstat, We setup a flat prior on F0 and F1, based on the values used to generate the signal:

from pyfstat import MCMCSearch

F0 = 30.0
F1 = -1e-10
F2 = 0
Alpha = 5e-3
Delta = 6e-2
tref = 362750407.0

tstart = 1000000000
duration = 100*86400
tend = tstart + duration

theta_prior = {'F0': {'type': 'unif', 'lower': F0-1e-4, 'upper': F0+1e-4},
               'F1': {'type': 'unif', 'lower': F1*(1+1e-3), 'upper': F1*(1-1e-3)},
               'F2': F2,
               'Alpha': Alpha,
               'Delta': Delta
               }

In this search, we will use paralllel tempering (to help the walkers move between the different peaks in the posterior).

ntemps = 2
log10temperature_min = -0.01
nwalkers = 100
nsteps = [500, 500]

mcmc = MCMCSearch('fully_coherent_search_using_MCMC_on_glitching_data', 'data',
                  sftfilepath='data/*_glitch*.sft',
                  theta_prior=theta_prior, tref=tref, tstart=tstart, tend=tend,
                  nsteps=nsteps, nwalkers=nwalkers, ntemps=ntemps,
                  log10temperature_min=log10temperature_min)
mcmc.run()
mcmc.plot_corner(add_prior=True)

Running this example, we obtain traces of the walkers like this:

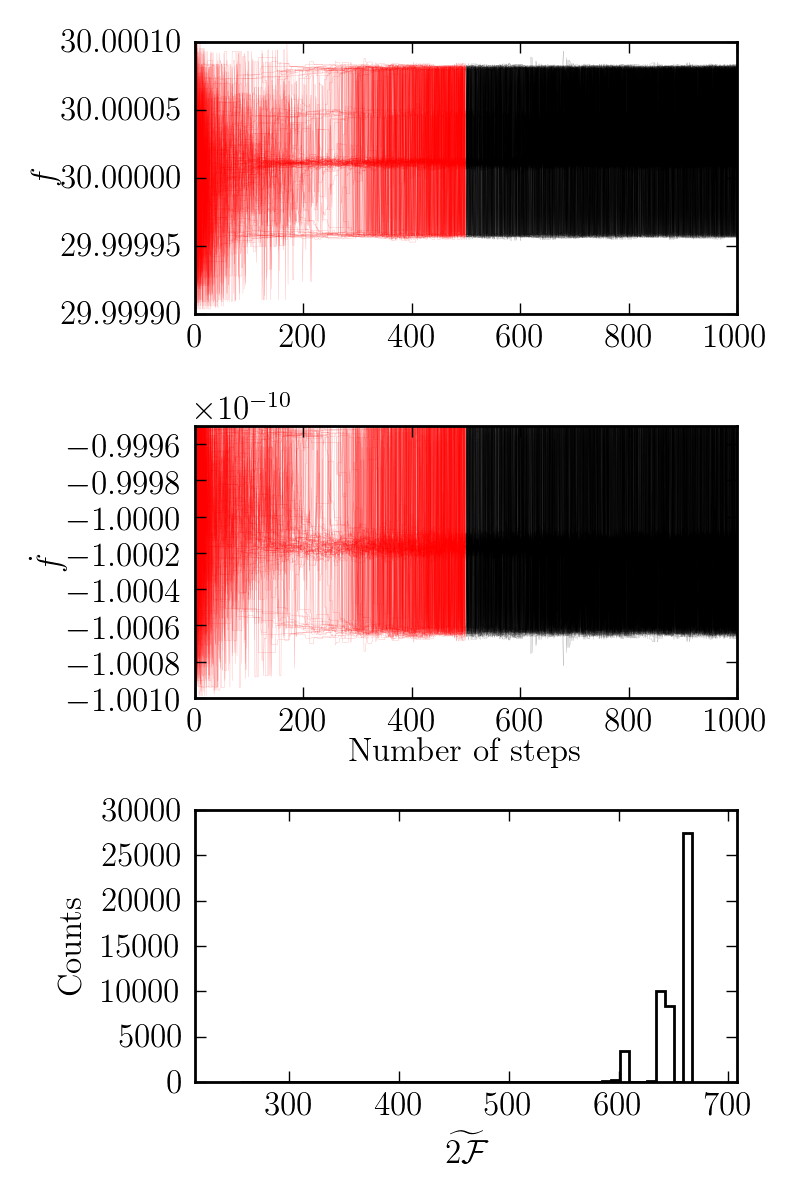
Although it is not obvious at first, the large widths of these traces in fact show that the walkers are jumping between multiple peaks (for both F0 and `F1): this is possible, due to the tuning of the parallel tempering. To see this clearly, we also plot the corner plot:

From this corner plot, we that unlike the in the single glitch fully-coherent search, the posterior, even after a large number of steps, is multimodal. However, these two peaks do not correspond exactly to the two frequencies before and after the glitch, which would be 30 and 30+4e5 (to see this, see how the data is generated). This is partly due to the noise and partly due to the fact that the maximum detection statistic in the case of glitches can occur at point in between the two frequencies. Moreover, we see bimodality in F1, which did does not change during the glitch.

>>> mcmc.print_summary()
Max twoF: 422.97

That is, compared to the basic search (on a smooth signal) which had a twoF of ~1764 (in agreement with the predicted twoF), we have lost a large fraction of the SNR due to the glitch.